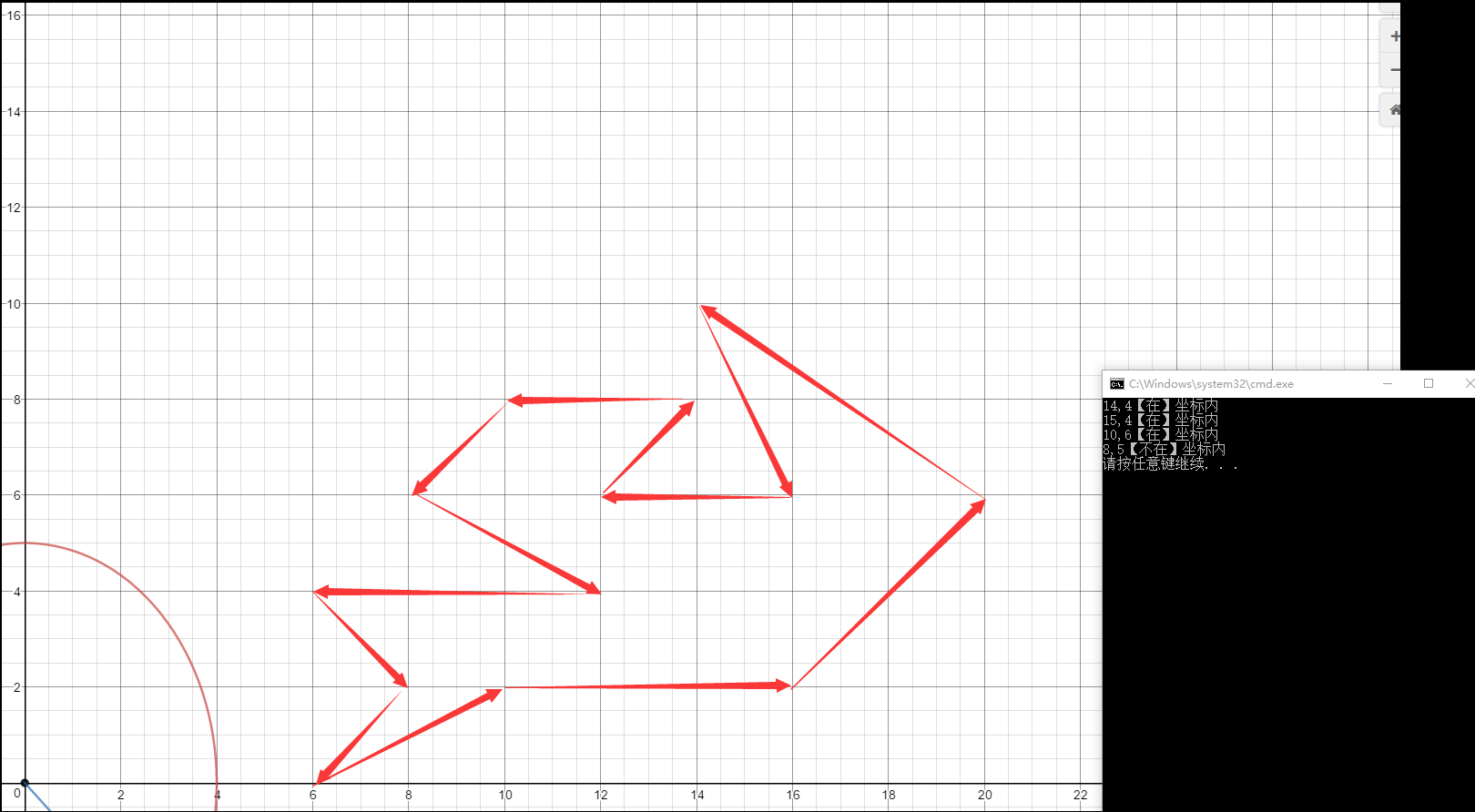
判断一点是否在不规则图像的内部,如下图是由一个个点组成的不规则图像,判断某一点是否在不规则矩形内部,先上效果图
算法实现如下,算法简单,亲试有效
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 | public class PositionAlgorithmHelper { /// <summary> /// 判断当前位置是否在不规则形状里面 /// </summary> /// <param name="nvert">不规则形状的定点数</param> /// <param name="vertx">当前x坐标</param> /// <param name="verty">当前y坐标</param> /// <param name="testx">不规则形状x坐标集合</param> /// <param name="testy">不规则形状y坐标集合</param> /// <returns></returns> public static bool PositionPnpoly( int nvert, List< double > vertx, List< double > verty, double testx, double testy) { int i, j, c = 0; for (i = 0, j = nvert - 1; i < nvert; j = i++) { if (((verty[i] > testy) != (verty[j] > testy)) && (testx < (vertx[j] - vertx[i]) * (testy - verty[i]) / (verty[j] - verty[i]) + vertx[i])) { c = 1 + c; ; } } if (c % 2 == 0) { return false ; } else { return true ; } } } |
用上图坐标进行测试:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 | class Program { static void Main( string [] args) { test1(); } /// <summary> /// test1 /// </summary> public static void test1() { //不规则图像坐标 List<Position> position = new List<Position>(); position.Add( new Position() { x = 6, y = 0 }); position.Add( new Position() { x = 10, y = 2 }); position.Add( new Position() { x = 16, y = 2 }); position.Add( new Position() { x = 20, y = 6 }); position.Add( new Position() { x = 14, y = 10 }); position.Add( new Position() { x = 16, y = 6 }); position.Add( new Position() { x = 12, y = 6 }); position.Add( new Position() { x = 14, y = 8 }); position.Add( new Position() { x = 10, y = 8 }); position.Add( new Position() { x = 8, y = 6 }); position.Add( new Position() { x = 12, y = 4 }); position.Add( new Position() { x = 6, y = 4 }); position.Add( new Position() { x = 8, y = 2 }); //用户当前位置坐标 List<Position> userPositions = new List<Position>(); userPositions.Add( new Position() { x = 14, y = 4 }); userPositions.Add( new Position() { x = 15, y = 4 }); userPositions.Add( new Position() { x = 10, y = 6 }); userPositions.Add( new Position() { x = 8, y = 5 }); //不规则图像x坐标集合 List< double > xList = position.Select(x => x.x).ToList(); //不规则图像y坐标集合 List< double > yList = position.Select(x => x.y).ToList(); foreach ( var userPosition in userPositions) { bool result = PositionAlgorithmHelper.PositionPnpoly(position.Count, xList, yList, userPosition.x, userPosition.y); if (result) { Console.WriteLine( string .Format( "{0},{1}【在】坐标内" , userPosition.x, userPosition.y)); } else { Console.WriteLine( string .Format( "{0},{1}【不在】坐标内" , userPosition.x, userPosition.y)); } } } } |
另外两种方式:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 | /// <summary> /// 判断点是否在多边形内. /// ----------原理---------- /// 注意到如果从P作水平向左的射线的话,如果P在多边形内部,那么这条射线与多边形的交点必为奇数, /// 如果P在多边形外部,则交点个数必为偶数(0也在内)。 /// 所以,我们可以顺序考虑多边形的每条边,求出交点的总个数。还有一些特殊情况要考虑。假如考虑边(P1,P2), /// 1)如果射线正好穿过P1或者P2,那么这个交点会被算作2次,处理办法是如果P的从坐标与P1,P2中较小的纵坐标相同,则直接忽略这种情况 /// 2)如果射线水平,则射线要么与其无交点,要么有无数个,这种情况也直接忽略。 /// 3)如果射线竖直,而P0的横坐标小于P1,P2的横坐标,则必然相交。 /// 4)再判断相交之前,先判断P是否在边(P1,P2)的上面,如果在,则直接得出结论:P再多边形内部。 /// </summary> /// <param name="checkPoint">要判断的点</param> /// <param name="polygonPoints">多边形的顶点</param> /// <returns></returns> public static bool IsInPolygon2(Position checkPoint, List<Position> polygonPoints) { int counter = 0; int i; double xinters; Position p1, p2; int pointCount = polygonPoints.Count; p1 = polygonPoints[0]; for (i = 1; i <= pointCount; i++) { p2 = polygonPoints[i % pointCount]; if (checkPoint.y > Math.Min(p1.y, p2.y) //校验点的Y大于线段端点的最小Y && checkPoint.y <= Math.Max(p1.y, p2.y)) //校验点的Y小于线段端点的最大Y { if (checkPoint.x <= Math.Max(p1.x, p2.x)) //校验点的X小于等线段端点的最大X(使用校验点的左射线判断). { if (p1.y != p2.y) //线段不平行于X轴 { xinters = (checkPoint.y - p1.y) * (p2.x - p1.x) / (p2.y - p1.y) + p1.x; if (p1.x == p2.x || checkPoint.x <= xinters) { counter++; } } } } p1 = p2; } if (counter % 2 == 0) { return false ; } else { return true ; } } /// <summary> /// 判断点是否在多边形内. /// ----------原理---------- /// 注意到如果从P作水平向左的射线的话,如果P在多边形内部,那么这条射线与多边形的交点必为奇数, /// 如果P在多边形外部,则交点个数必为偶数(0也在内)。 /// </summary> /// <param name="checkPoint">要判断的点</param> /// <param name="polygonPoints">多边形的顶点</param> /// <returns></returns> public static bool IsInPolygon(Position checkPoint, List<Position> polygonPoints) { bool inside = false ; int pointCount = polygonPoints.Count; Position p1, p2; for ( int i = 0, j = pointCount - 1; i < pointCount; j = i, i++) //第一个点和最后一个点作为第一条线,之后是第一个点和第二个点作为第二条线,之后是第二个点与第三个点,第三个点与第四个点... { p1 = polygonPoints[i]; p2 = polygonPoints[j]; if (checkPoint.y < p2.y) { //p2在射线之上 if (p1.y <= checkPoint.y) { //p1正好在射线中或者射线下方 if ((checkPoint.y - p1.y) * (p2.x - p1.x) > (checkPoint.x - p1.x) * (p2.y - p1.y)) //斜率判断,在P1和P2之间且在P1P2右侧 { //射线与多边形交点为奇数时则在多边形之内,若为偶数个交点时则在多边形之外。 //由于inside初始值为false,即交点数为零。所以当有第一个交点时,则必为奇数,则在内部,此时为inside=(!inside) //所以当有第二个交点时,则必为偶数,则在外部,此时为inside=(!inside) inside = (!inside); } } } else if (checkPoint.y < p1.y) { //p2正好在射线中或者在射线下方,p1在射线上 if ((checkPoint.y - p1.y) * (p2.x - p1.x) < (checkPoint.x - p1.x) * (p2.y - p1.y)) //斜率判断,在P1和P2之间且在P1P2右侧 { inside = (!inside); } } } return inside; } |
/// <summary> /// 判断点是否在多边形内. /// ----------原理---------- /// 注意到如果从P作水平向左的射线的话,如果P在多边形内部,那么这条射线与多边形的交点必为奇数, /// 如果P在多边形外部,则交点个数必为偶数(0也在内)。 /// 所以,我们可以顺序考虑多边形的每条边,求出交点的总个数。还有一些特殊情况要考虑。假如考虑边(P1,P2), /// 1)如果射线正好穿过P1或者P2,那么这个交点会被算作2次,处理办法是如果P的从坐标与P1,P2中较小的纵坐标相同,则直接忽略这种情况 /// 2)如果射线水平,则射线要么与其无交点,要么有无数个,这种情况也直接忽略。 /// 3)如果射线竖直,而P0的横坐标小于P1,P2的横坐标,则必然相交。 /// 4)再判断相交之前,先判断P是否在边(P1,P2)的上面,如果在,则直接得出结论:P再多边形内部。 /// </summary> /// <param name="checkPoint">要判断的点</param> /// <param name="polygonPoints">多边形的顶点</param> /// <returns></returns> public static bool IsInPolygon2(Position checkPoint, List<Position> polygonPoints) { int counter = 0; int i; double xinters; Position p1, p2; int pointCount = polygonPoints.Count; p1 = polygonPoints[0]; for (i = 1; i <= pointCount; i++) { p2 = polygonPoints[i % pointCount]; if (checkPoint.y > Math.Min(p1.y, p2.y)//校验点的Y大于线段端点的最小Y && checkPoint.y <= Math.Max(p1.y, p2.y))//校验点的Y小于线段端点的最大Y { if (checkPoint.x <= Math.Max(p1.x, p2.x))//校验点的X小于等线段端点的最大X(使用校验点的左射线判断). { if (p1.y != p2.y)//线段不平行于X轴 { xinters = (checkPoint.y - p1.y) * (p2.x - p1.x) / (p2.y - p1.y) + p1.x; if (p1.x == p2.x || checkPoint.x <= xinters) { counter++; } } }
} p1 = p2; } if (counter % 2 == 0) { return false; } else { return true; } } /// <summary> /// 判断点是否在多边形内. /// ----------原理---------- /// 注意到如果从P作水平向左的射线的话,如果P在多边形内部,那么这条射线与多边形的交点必为奇数, /// 如果P在多边形外部,则交点个数必为偶数(0也在内)。 /// </summary> /// <param name="checkPoint">要判断的点</param> /// <param name="polygonPoints">多边形的顶点</param> /// <returns></returns> public static bool IsInPolygon(Position checkPoint, List<Position> polygonPoints) { bool inside = false; int pointCount = polygonPoints.Count; Position p1, p2; for (int i = 0, j = pointCount - 1; i < pointCount; j = i, i++)//第一个点和最后一个点作为第一条线,之后是第一个点和第二个点作为第二条线,之后是第二个点与第三个点,第三个点与第四个点... { p1 = polygonPoints[i]; p2 = polygonPoints[j]; if (checkPoint.y < p2.y) {//p2在射线之上 if (p1.y <= checkPoint.y) {//p1正好在射线中或者射线下方 if ((checkPoint.y - p1.y) * (p2.x - p1.x) > (checkPoint.x - p1.x) * (p2.y - p1.y))//斜率判断,在P1和P2之间且在P1P2右侧 { //射线与多边形交点为奇数时则在多边形之内,若为偶数个交点时则在多边形之外。 //由于inside初始值为false,即交点数为零。所以当有第一个交点时,则必为奇数,则在内部,此时为inside=(!inside) //所以当有第二个交点时,则必为偶数,则在外部,此时为inside=(!inside) inside = (!inside); } } } else if (checkPoint.y < p1.y) { //p2正好在射线中或者在射线下方,p1在射线上 if ((checkPoint.y - p1.y) * (p2.x - p1.x) < (checkPoint.x - p1.x) * (p2.y - p1.y))//斜率判断,在P1和P2之间且在P1P2右侧 { inside = (!inside); } } } return inside; }